[자료구조] Binary Search Tree(이진 탐색 트리) with Swift - 구현

안녕하세요. 개발하는 정주입니다.

 

오늘은 "Binary Search Tree(이진 탐색 트리) with Swift"을 정리하였습니다.

지난 포스팅에서는 트리의 개념에 대해 배웠습니다.

이번 포스팅에서는 Swift를 이용해 직접 구현해 보았습니다.

 

틀린 점이 있다면 댓글로 알려주세요!

---

Swift로 이진 탐색 트리 구현하기

Swift로 이진 탐색 트리를 구현해보겠습니다.

트리의 구조를 보면 알겠지만 연결 리스트를 응용하여 구현합니다.

코드는 맨 아래 전체 코드도 첨부하였고 깃허브에서 확인도 가능합니다.

 

트리 출력하기

트리를 출력하는 코드는 다른 분의 좋은 코드를 가져왔습니다.

devmjun.github.io/archive/BinarySearchTree

extension BinarySearchTree {
    func drawDiagram() {
        print(diagram(for: self.root))
    }
    
    private func diagram(for node: Node?,
                         _ top: String = "",
                         _ root: String = "",
                         _ bottom: String = "") -> String {
        guard let node = node else {
            return root + "nil\n"
        }
        if node.left == nil && node.right == nil {
            return root + "\(node.data)\n"
        }
        return diagram(for: node.right, top + " ", top + "┌──", top + "│ ")
            + root + "\(node.data)\n"
            + diagram(for: node.left, bottom + "│ ", bottom + "└──", bottom + " ")
    }
}

 

---

Node 클래스

트리의 Node를 나타내는 클래스입니다.

class Node {
    var data: Int //데이터는 항상 존재해야 한다.
    var parent: Node?
    var left: Node?
    var right: Node?
    
    init(data: Int) {
        self.data = data
    }
    
    var isRoot: Bool {
        return parent == nil
    }
    
    var isLeaf: Bool {
        return left == nil && right == nil
    }
    
    var isFull: Bool {
        return left != nil && right != nil
    }
}

• data : 노드의 데이터
• parent : 노드의 부모
• left, right : 왼쪽 자식 노드, 오른쪽 자식 노드
• isRoot : 노드가 root 노드인지 체크
• isLeaf : 노드가 leaf 노드인지 체크
• isFull : 노드가 포화 상태인지 체크

 

---

BinarySearchTree 클래스

BST 클래스를 구현해 봅시다.

코드를 보려면 각 문단의 더보기를 누르세요.

root 노드

class BinarySearchTree {
    var root: Node?
    ...
}

트리의 root 노드를 나타냅니다.

 

삽입 (insert)

BST에서 삽입 연산은 탐색 + 삽입 연산으로 시간 복잡도는 O(log N) + O(1)입니다.

삽입할 데이터가 이미 BST에 있으면 삽입하지 않습니다.

 

먼저 값을 삽입할 위치를 탐색해야 합니다.

1. 탐색은 항상 root에서 시작합니다.
2. 삽입할 data가 현재 노드의 data보다 작다면 왼쪽 노드로 이동합니다. 
   삽입할 data가 현재 노드의 data보다 크다면 오른쪽 노드로 이동합니다.
3. 이동할 노드가 비어 있다면 노드를 생성하여 데이터를 삽입하고 parent를 설정합니다.

func insert(_ data: Int) {
    guard let root = root else {
        self.root = Node(data: data)
        return
    }

    var currentNode: Node = root
    while true {
        //BST의 값은 유일해야 한다.
        if currentNode.data == data {
            return
        }

        if currentNode.data > data {
            //삽입할 값이 현재 노드의 값보다 작으면 왼쪽 노드로 이동한다.
            guard let nextLeftNode = currentNode.left else {
                //왼쪽 노드가 비어 있으면 새로운 노드를 생성, 삽입한다.
                currentNode.left = Node.init(data: data)
                currentNode.left?.parent = currentNode
                return
            }

            currentNode = nextLeftNode
        } else {
            //삽입할 값이 현재 노드의 값보다 크면 오른쪽 노드로 이동한다.
            guard let nextRightNode = currentNode.right else {
                //오른쪽 노드가 비어 있으면 새로운 노드를 생성, 삽입한다.
                currentNode.right = Node.init(data: data)
                currentNode.right?.parent = currentNode
                return
            }

            currentNode = nextRightNode
        }
    }
}

 

삽입 (insert) 테스트

15, 10, 9, 20, 13, 18, 16 순서로 insert를 해보았습니다.

let binarySearchTree = BinarySearchTree()

binarySearchTree.insert(15)
binarySearchTree.insert(10)
binarySearchTree.insert(9)
binarySearchTree.insert(20)
binarySearchTree.insert(13)
binarySearchTree.insert(18)
binarySearchTree.insert(16)

binarySearchTree.drawDiagram()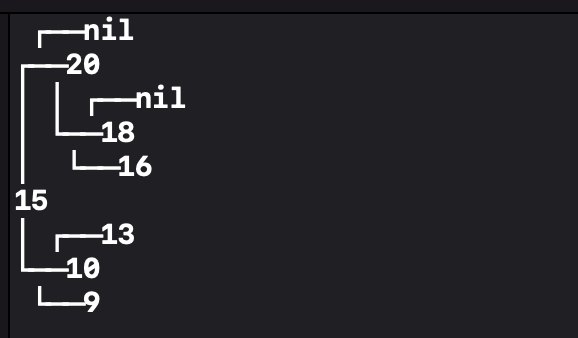

15를 root로 가지고 데이터가 정렬된 상태로 제대로 삽입이 되었습니다.

 

탐색 (search)

BST에서 data 노드가 있는지 확인하고 있다면 그 노드를 return 합니다.

BST는 반씩 제외시키며 탐색하기 때문에 시간 복잡도는 O(log N)입니다.

탐색 알고리즘은 아래와 같습니다. 재귀 호출을 이용해도 되지만 반복문을 이용했습니다.

1. 탐색은 항상 root부터 시작합니다.
2. 현재 노드의 데이터가 탐색 데이터와 동일하면 현재 노드를 return 합니다.
3. 탐색 데이터가 현재 노드의 데이터보다 작다면 왼쪽 노드로 이동하여 탐색합니다.
4. 탐색 데이터가 현재 노드의 데이터보다 크다면 오른쪽 노드로 이동하여 탐색합니다.

func search(_ data: Int) -> Node? {
    var currentNode: Node? = root
    while let node = currentNode {
        //찾는 값이 있으면 break
        if node.data == data { break }

        //이진 탐색
        currentNode = (node.data > data) ? node.left : node.right
    }

    return currentNode
}

 

탐색 (search) 테스트

탐색이 제대로 동작하는지 확인해 봅시다.

insert에서 사용한 트리에서 값을 찾아봅시다.

let isExist20: Bool = (binarySearchTree.search(20) != nil)
let isExist30: Bool = (binarySearchTree.search(30) != nil)
print("isExist20: \(isExist20) / isExist30: \(isExist30)")

//isExist20: true / isExist30: false

20은 트리에 존재하기 때문에 true, 30은 트리에 없기 때문에 false가 출력됩니다.

 

삭제 (remove)

BST의 노드 삭제를 구현해봅시다.

BST의 노드 삭제는 아주 복잡합니다.. ㅠㅠ

노드를 삭제한 후에도 트리의 정렬 규칙이 지켜져야 하므로 재정렬을 해야 하기 때문인데요.

케이스에 따라 하나하나 구현해 봅시다.

 

루트 노드 삭제 케이스

1. 루트 노드만 존재할 때 루트 노드를 삭제하는 경우

아주 심플한 케이스입니다.

루트 노드만 존재할 때 루트 노드를 삭제하는 경우 root만 nil로 초기화하면 삭제가 완료됩니다.

root = nil

 

2. 루트 노드의 자식 노드가 1개인 경우

루트 노드가 왼쪽 혹은 오른쪽 1개의 노드만 가지고 있는 경우입니다.

 

if node.left != nil { //왼쪽 노드만 있는 경우
    node.left?.parent = nil
    root = node.left
} else if node.right != nil { //오른쪽 노드만 있는 경우
    node.right?.parent = nil
    root = node.right
}

이때 루트 노드를 삭제하는 것은 한 쪽 자식 서브 트리의 root를 전체 BST의 root로 설정하면 됩니다.

이 방법이 가능한 이유는 BST의 서브 트리가 이미 정렬되어 있는 상태이기 때문입니다.

 

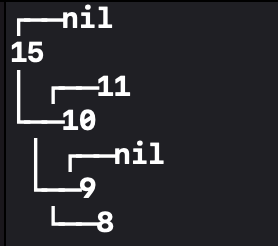
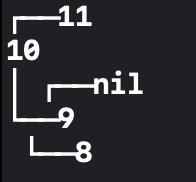
root가 15이고 왼쪽 노드만 가지고 있는 BST입니다.

이때 15를 remove하면 10을 root로 설정하기만 하면 쉽게 루트 노드를 삭제할 수 있습니다.

 

3. 루트 노드의 자식 노드가 2개인 경우

루트 노드가 Full인 경우인데 이때는 일반 노드의 삭제와 동일합니다.

 

var changeNode = node.right!
while let nextNode = changeNode.left {
    changeNode = nextNode
}

changeNode.left = root?.left
changeNode.right = root?.right
root = changeNode

changeNode.parent?.left = nil

root를 삭제한 후에도 변경된 root의 값보다 왼쪽은 작아야 하고 오른쪽은 커야 합니다.

root의 오른쪽 서브 트리 중 가장 작은 노드를 root로 만들면 이 규칙을 지킬 수 있습니다.

 

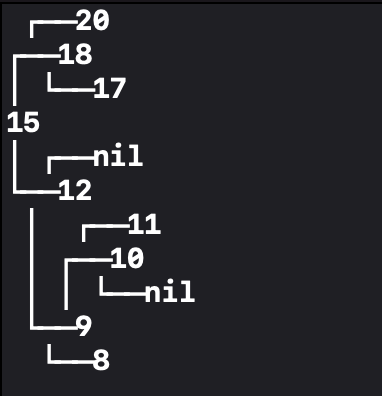
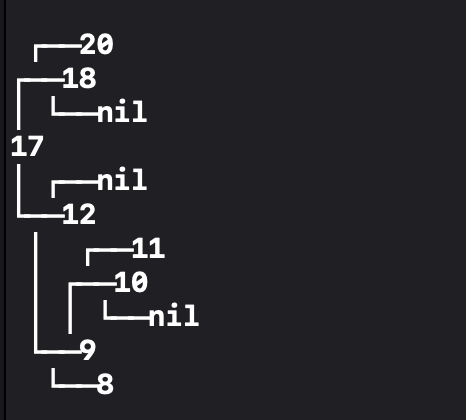
왼쪽 BST에서 root인 15를 삭제합니다.

root의 오른쪽 서브 트리에서 가장 작은 값인 17이 새로운 root로 채택되어

새로운 BST를 만들었습니다.

 

 

Leaf 노드 삭제하기

Leaf 노드를 삭제하는 것은 간다 합니다.

if node.parent?.left?.data == data { //왼쪽 노드일 경우
    node.parent?.left = nil
} else { //오른쪽 노드일 경우
    node.parent?.right = nil
}
node.parent = nil

코드에서는 삭제할 Leaf 노드가 왼쪽 노드인지 오른쪽 노드인지 알 수 없습니다.

그래서 prarent의 양쪽 자식 데이터와 Leaf 노드의 데이터를 비교하여 어떤 방향인지 확인합니다.

 

부모의 left의 데이터와 같다면 left를 nil로 초기화해주고

 

부모의 right의 데이터와 같다면 right를 nil로 초기화해줍니다.

각 노드를 초기화한 후에는 node의 parent를 nil로 초기화하여 연결을 끊어줍니다.

 

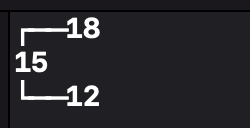
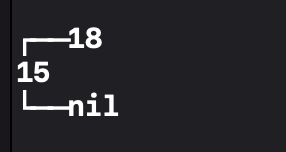
간단한 BST입니다. 

오른쪽 BST에서 Leaf 노드인 12를 삭제하면 왼쪽처럼 잘 사라지는 것을 볼 수 있습니다.

 

내부 노드 삭제 케이스

내부 노드를 삭제해 봅시다.

루트 노드, Leaf 노드보다 조금 더 복잡합니다... ㅠㅠ

 

1. 자식 노드가 1개인 경우

자식 노드가 1개인 경우는 왼쪽 노드가 있는 경우와 오른쪽 노드가 있는 경우로 나뉩니다.

• 왼쪽 서브 트리가 있는 경우
  
  • 지울 값이 부모 값보다 작다면 부모의 왼쪽에 지울 노드의 왼쪽 서브 트리를 붙인다.
  • 지울 값이 부모 값보다 크다면 부모의 오른쪽에 지울 노드의 왼쪽 서브 트리를 붙인다.
• 오른쪽 서브 트리가 있는 경우
  
  • 지울 값이 부모 값보다 작다면 부모의 왼쪽에 지울 노드의 오른쪽 서브 트리를 붙인다.
  • 지울 값이 부모 값보다 크다면 부모의 오른쪽에 지울 노드의 오른쪽 서브 트리를 붙인다.

이 알고리즘을 아래처럼 코드로 작성할 수 있습니다.

func removeSingleChildNode(_ node: Node, data: Int) {
    guard let parent = node.parent else { return }

    if node.left != nil { //target의 왼쪽 노드가 존재하는 경우
        if parent.data > data {
            parent.left = node.left
        } else {
            parent.right = node.left
        }
        node.left?.parent = parent
    } else { //target의 오른쪽 노드가 존재하는 경우
        if parent.data > data {
            parent.left = node.right
        } else {
            parent.right = node.right
        }
        node.right?.parent = parent
    }
}

 

코드가 잘 작동하는지 테스트해보겠습니다.

 

왼쪽 트리에서 10을 지워보겠습니다.

10은 왼쪽 자식인 9를 가지고 있습니다.

이 9가 12보다 작기 때문에 12의 왼쪽에 잘 붙은 것을 볼 수 있습니다.

굿굿~

 

2. 자식 노드가 2개인 경우

자식 노드가 2개인 경우는 루트 노드에서 본 것과 같습니다.

삭제할 노드를 새로운 노드로 교체해줘야 하는데요.

삭제할 노드의 오른쪽 서브 트리에서 가장 작은 노드를 새로운 노드로 채택합니다.

 

교체할 노드의 값이 삭제할 노드의 부모의 값보다 작으면 왼쪽으로, 크면 오른쪽으로 붙입니다.

 

func removeFullNode(_ node: Node, data: Int) {
    guard let parent = node.parent else { return }
    guard let rightNode = node.right else { return }

    var changeNode = rightNode
    while let nextNode = changeNode.left {
        changeNode.parent = changeNode
        changeNode = nextNode
    }

    if let changeChildNode = changeNode.right {
        //변경할 노드가 leaf가 아닌 경우 -> right 노드가 있는 경우
        changeNode.parent?.right = changeChildNode
        changeChildNode.parent = changeNode
    } else {
        changeNode.parent?.right = nil
    }

    if parent.data > changeNode.data {
        parent.left = changeNode
    } else {
        parent.right = changeNode
    }
    changeNode.parent = parent

    changeNode.left = node.left
    changeNode.right = node.right
}

 

잘 동작하는지 확인해 봅시다.

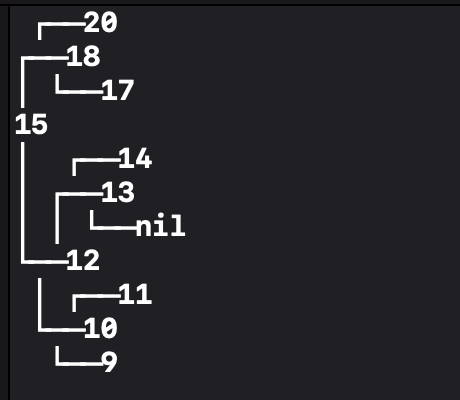
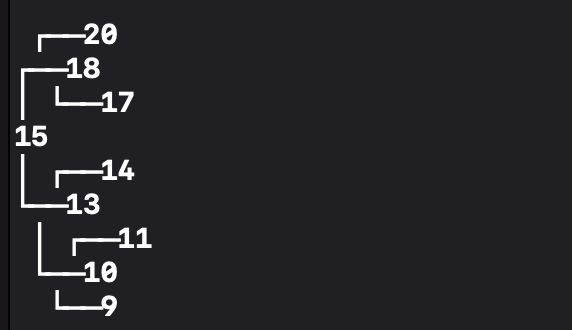
왼쪽 BST에서 중간의 12 노드를 삭제해 봅시다.

12가 삭제되고 그 자리에 12의 오른쪽 노드에서 가장 작은 값인 13 노드가 들어갑니다.

13은 12의 부모인 15보다 작기 때문에 15의 왼쪽에 붙었습니다.

 

결과로 나온 BST는 제대로 정렬된 것을 볼 수 있습니다.

 

---

전체 코드

전체 코드입니다.

너무 길어서 접은 글로 삽입했으니 더 보기를 눌러 확인해 보세요.

import Foundation

class Node {
    var data: Int //데이터는 항상 존재해야 한다.
    var parent: Node?
    var left: Node?
    var right: Node?
    
    init(data: Int) {
        self.data = data
    }
    
    var isRoot: Bool {
        return parent == nil
    }
    
    var isLeaf: Bool {
        return left == nil && right == nil
    }
    
    var isFull: Bool {
        return left != nil && right != nil
    }
}

class BinarySearchTree {
    var root: Node?
    
    func insert(_ data: Int) {
        guard let root = root else {
            self.root = Node(data: data)
            return
        }

        var currentNode: Node = root
        while true {
            //BST의 값은 유일해야 한다.
            if currentNode.data == data {
                return
            }
         
            if currentNode.data > data {
                //삽입할 값이 현재 노드의 값보다 작으면 왼쪽 노드로 이동한다.
                guard let nextLeftNode = currentNode.left else {
                    //왼쪽 노드가 비어 있으면 새로운 노드를 생성, 삽입한다.
                    currentNode.left = Node.init(data: data)
                    currentNode.left?.parent = currentNode
                    return
                }
                
                currentNode = nextLeftNode
            } else {
                //삽입할 값이 현재 노드의 값보다 크면 오른쪽 노드로 이동한다.
                guard let nextRightNode = currentNode.right else {
                    //오른쪽 노드가 비어 있으면 새로운 노드를 생성, 삽입한다.
                    currentNode.right = Node.init(data: data)
                    currentNode.right?.parent = currentNode
                    return
                }
                
                currentNode = nextRightNode
            }
        }
    }
    
    func remove(_ data: Int) -> Bool {
        guard let targetNode = search(data) else { //탐색 실패
            return false
        }
        
        if targetNode.isRoot { //root 노드를 지우는 경우
            removeRoot(targetNode)
        } else if targetNode.isLeaf { //Leaf 노드인 경우
            removeLeaf(targetNode, data: data)
        } else {
            if targetNode.isFull { //자식 노드가 2개인 경우
                removeFullNode(targetNode, data: data)
            } else { //자식 노드가 1개인 경우
                removeSingleChildNode(targetNode, data: data)
            }
        }
        
        return true
    }
    
    private func removeRoot(_ node: Node) {
        if node.isLeaf {
            root = nil
        } else if node.isFull {
            var changeNode = node.right!
            while let nextNode = changeNode.left {
                changeNode = nextNode
            }
            
            changeNode.left = root?.left
            changeNode.right = root?.right
            root = changeNode
            
            changeNode.parent?.left = nil
        } else {
            if node.left != nil { //왼쪽 노드만 있는 경우
                node.left?.parent = nil
                root = node.left
            } else if node.right != nil { //오른쪽 노드만 있는 경우
                node.right?.parent = nil
                root = node.right
            }
        }
    }
    
    private func removeLeaf(_ node: Node, data: Int) {
        if node.parent?.left?.data == data { //왼쪽 노드일 경우
            node.parent?.left = nil
        } else { //오른쪽 노드일 경우
            node.parent?.right = nil
        }
        node.parent = nil
    }
    
    private func removeSingleChildNode(_ node: Node, data: Int) {
        guard let parent = node.parent else { return }
        
        if node.left != nil { //target의 왼쪽 노드가 존재하는 경우
            if parent.data > data {
                parent.left = node.left
            } else {
                parent.right = node.left
            }
            node.left?.parent = parent
        } else { //target의 오른쪽 노드가 존재하는 경우
            if parent.data > data {
                parent.left = node.right
            } else {
                parent.right = node.right
            }
            node.right?.parent = parent
        }
    }
    
    private func removeFullNode(_ node: Node, data: Int) {
        guard let parent = node.parent else { return }
        guard let rightNode = node.right else { return }
        
        var changeNode = rightNode
        while let nextNode = changeNode.left {
            changeNode.parent = changeNode
            changeNode = nextNode
        }
                
        if let changeChildNode = changeNode.right {
            //변경할 노드가 leaf가 아닌 경우 -> right 노드가 있는 경우
            changeNode.parent?.right = changeChildNode
            changeChildNode.parent = changeNode
        } else {
            changeNode.parent?.right = nil
        }
        
        if parent.data > changeNode.data {
            parent.left = changeNode
        } else {
            parent.right = changeNode
        }
        changeNode.parent = parent
        
        changeNode.left = node.left
        changeNode.right = node.right
    }
    
    func search(_ data: Int) -> Node? {
        var currentNode: Node? = root
        while let node = currentNode {
            //찾는 값이 있으면 break
            if node.data == data { break }
            
            //이진 탐색
            currentNode = (node.data > data) ? node.left : node.right
        }
        
        return currentNode
    }
}

extension BinarySearchTree {
    func drawDiagram() {
        print(diagram(for: self.root))
    }
    
    private func diagram(for node: Node?,
                         _ top: String = "",
                         _ root: String = "",
                         _ bottom: String = "") -> String {
        guard let node = node else {
            return root + "nil\n"
        }
        if node.left == nil && node.right == nil {
            return root + "\(node.data)\n"
        }
        return diagram(for: node.right, top + " ", top + "┌──", top + "│ ")
            + root + "\(node.data)\n"
            + diagram(for: node.left, bottom + "│ ", bottom + "└──", bottom + " ")
    }
}

let binarySearchTree = BinarySearchTree()

binarySearchTree.insert(15)
binarySearchTree.insert(18)
binarySearchTree.insert(20)
binarySearchTree.insert(12)
binarySearchTree.insert(10)
binarySearchTree.insert(11)
binarySearchTree.insert(17)
binarySearchTree.insert(13)
binarySearchTree.insert(9)
binarySearchTree.insert(14)

binarySearchTree.drawDiagram()

binarySearchTree.remove(12)
binarySearchTree.drawDiagram()

 

---

 

마무리

이진 탐색 트리, BST를 Swift로 구현해보았습니다.

자료 구조 포스팅 중 제일 난이도가 있었던 것 같습니다.

이걸.... 알고리즘 코딩 테스트에 쓰려면 엄청난 연습을 해야겠네요 ㅎㅎ...

 

파이팅입니다!

 

감사합니다!

---

출처

https://babbab2.tistory.com/91?category=908011

 

잘못된 점이 있다면 댓글로 알려주시면 감사하겠습니다.

감사합니다.