[자료구조] Linked List(링크드 리스트) with Swift

안녕하세요. 개발하는 정주입니다.

 

오늘은 "Linked List(링크드 리스트)"을 정리하였습니다.

최근에 코딩 테스트를 준비하기 위해 알고리즘 포스팅만 잔뜩 적었는데요.

오랜만에 자료구조를 포스팅 하려니 설렙니다.

 

---

Singly linked list(링크드 리스트)란?

링크드 리스트(연결 리스트)는 노드가 연결되어 있는 자료구조입니다.

각 노드는 다음 노드를 가리키는 포인터와 노드의 데이터를 가지고 있습니다.

이 포스팅에서 수식어가 없는 링크드 리스트는 단방향 링크드 리스트를 의미합니다.

[이미지 출처] geeksforgeeks

 

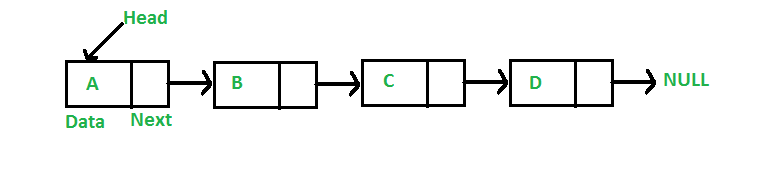
데이터가 연속적으로 연결되어 있는 자료구조이기 때문에 배열과 많이 비교가 되는데요.

저도 짧게 다뤄보며 이전에 작성한 큐를 링크드 리스트로 구현했을 때의 장단점도 살펴보겠습니다.

 

---

배열과 링크드 리스트의 차이

배열

앞서 포스팅한 배열은 데이터가 연속적으로 저장되어 있습니다.

따라서 arr[0], arr[1]처럼 index를 이용해 데이터에 접근할 수 있죠.

이는 index만 알고 있다면 O(1)의 시간복잡도로 원소에 접근할 수 있다는 장점으로 이어집니다.

 

하지만 "연속적으로 저장된다"는 개념때문에 1~n-1번째 원소를 삭제할 때 연산의 오버헤드가 발생한다는 단점이 있습니다.

삭제한 자리를 채우기 위해 뒷 부분을 모두 앞으로 당겨와야 하기 때문입니다.

 

링크드 리스트

링크드 리스트는 현재 노드가 다음 노드의 주소를 가지고 있다는 점에 주목해야 합니다.

다음 노드의 위치를 가지고 있기 때문에 연속적으로 저장할 필요가 없습니다.

따라서 중간 삽입, 삭제를 해도 연산의 오버헤드가 발생하지 않아 O(1)의 시간복잡도로 할 수 있습니다.

(현실적으로 가장 기초적인 링크드 리스트는 탐색 후 삽입/삭제를 해야 하므로 O(n+1)입니다.)

 

하지만 index로 원소의 접근이 불가능하여 원소를 찾는데 O(n)의 시간 복잡도가 발생합니다.

(링크드 리스트의 원소 탐색 방법은 아래에서 자세히 살펴보겠습니다.)

이것은 극복하기 위해 더블 링크드 리스트같은 개선판(?)도 나왔는데 원소의 접근은 배열보다 느리다는 점은 같습니다.

 

정리하자면

배열은 원소에 접근하는 것은 빠르지만 중간 삽입/삭제가 느립니다.

링크드 리스트는 중간 삽입/삭제가 빠르지만 원소의 탐색이 느립니다.

 

아래에서 링크드 리스트를 사용하면 좋은 알고리즘 문제도 하나 소개해드리겠습니다.

 

---

Doubly linked list(양방향 링크드 리스트)

링크드 리스트에는 다양한 종류가 있습니다.

그 중에서 가장 대표적인 것이 양방향 연결 리스트입니다.

 

다른 링크드 리스트는 모두 링크드 리스트와 양방향 연결 리스트의 응용 버전이므로 따로 다루지 않습니다.

혹시 궁금하신 분들은 아래 링크를 참고해 주세요. (한국판 위키피디아에는 너무 간단하게 나와 있어 영문판으로 가져 왔습니다 ^^;;)

Linked list - Wikipedia

 

양방향 링크드 리스트의 탄생 이유

위에서 말했듯이 링크드 리스트는 단방향의 성격을 가집니다.

즉 n번째 원소를 찾기 위해서는 무조건 n-1개의 노드를 지나야 합니다.

또한 바로 직전의 노드로 역행하는 행위도 절대 불가능하죠.

 

이런 단점을 해소하기 위해 이전 노드를 알 수 있도록 한 양방향 링크드 리스트가 나왔습니다.

 

양방향 링크드 리스트의 장단점

이전 노드를 알 수 있다는 것이 별 거 아니라고 느껴질 수 있습니다.

하지만 이로 인해 탐색의 시간은 절반이 됩니다. 왜 그럴까요?

 

바로 마지막에서 역행하여 탐색할 수 있기 때문입니다.

예를 들어 길이가 10인 링크드 리스트에서 7번째 노드를 찾아간다고 합시다.

기존 링크드 리스트에서는 7회의 탐색이 있어야 7번째 노드를 찾을 수 있습니다.

하지만 이제는 마지막 노드에서 시작하여 3회의 탐색만으로 7번째 노드를 찾을 수 있습니다.

 

만약 cursor라는 개념을 이용하여 마지막 탐색 노드를 저장한다고 합시다.

4, 3, 5번째 노드를 차례대로 탐색한다고 합시다. 첫 번째 4번을 탐색하고 커서를 4번 노드로 설정합니다.

다음 3번 노드를 탐색할 때는 커서를 1회만 움직이면 되고 그 다음 5번 노드를 탐색할 때는 단 2회만 움직이면 됩니다.

 

이렇게 이전 노드를 알 수 있는 것만으로도 마지막 노드를 참조하는 것은 O(n)에서 O(1)이 되었고

중간 위치 노드의 탐색 시간은 두 배가량 줄었습니다. (O(n)이라는 것은 동일합니다.)

 

단점은 공간 복잡도가 상대적으로 좋지 않다는 것입니다.

각 노드에서 이전 노드까지 저장해야 하고 tail이라는 것도 알아야 하니 공간복잡도는 상대적으로 좋지 않습니다.

 

따라서 상황에 맞춰 단방향과 양방향을 선택해야 할 수 있어야 합니다.

 

---

링크드 리스트의 연산

링크드 리스트의 연산 중 노드 추가, 노드 삭제, 노드 탐색을 살펴 보겠습니다.

아래부터 설명하는 링크드 리스트는 단방향이며 맨 앞 노드를 나타내는 head, 맨 뒤 노드를 나타내는 tail을 가진다고 가정합니다.

 

노드 추가

링크드 리스트의 노드 추가 연산은 세 가지로 나뉩니다.

• 맨 앞 위치에 추가
• 중간 위치에 추가
• 맨 뒤 위치에 추가

맨 앞 위치에 추가

맨 앞 위치에 추가하는 연산은 head를 교체한다는 것과 같습니다.

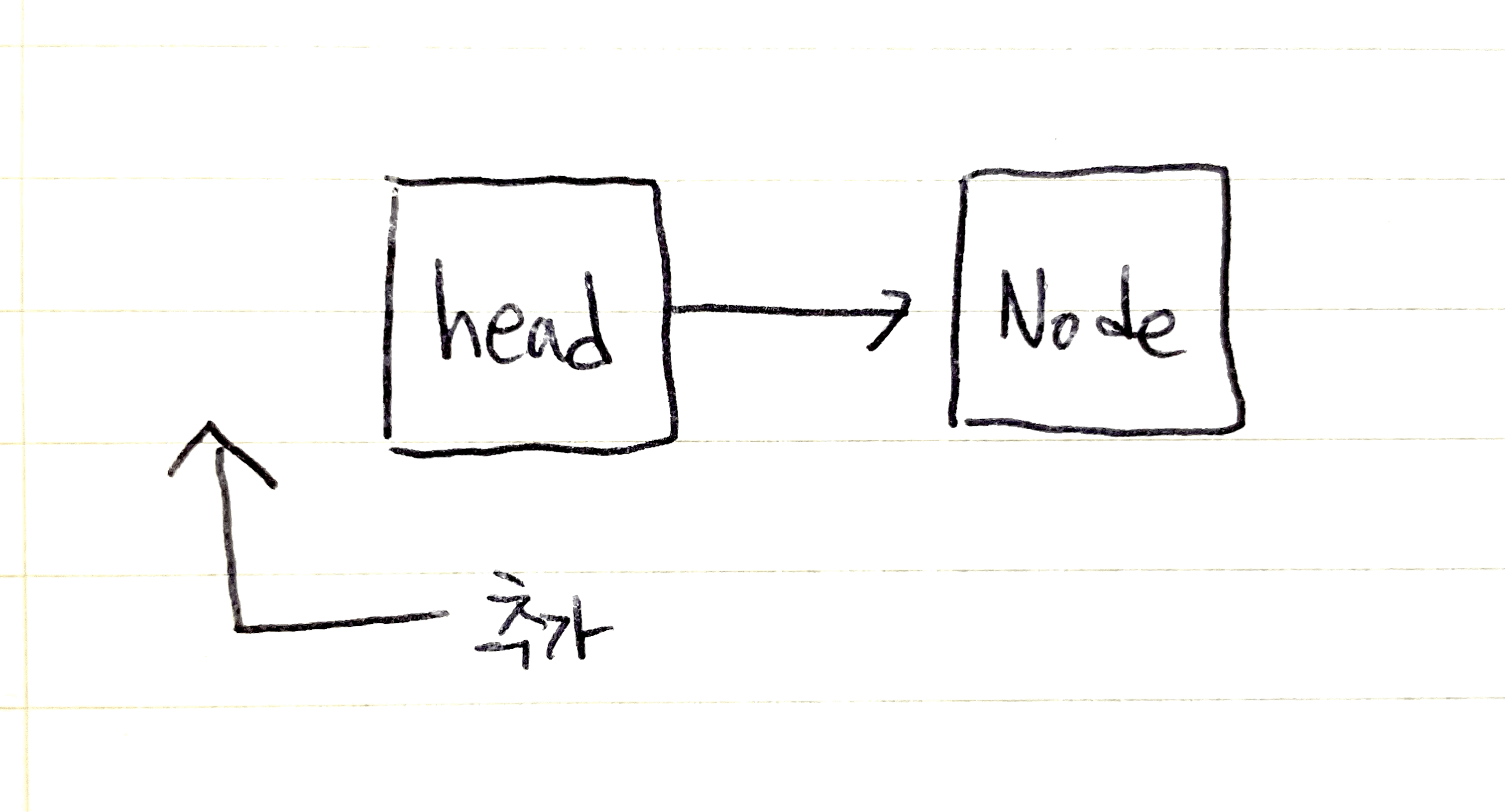
그림으로 나타내면 이런 형태입니다.

추가하는 노드의 next를 이전 head로 설정하고 새로운 노드를 head로 설정합니다.

이 간단한 작업만으로 맨 앞 위치에 추가 연산이 끝납니다.

중간 위치에 추가

중간 위치에 추가하는 것은 head나 tail을 교체하는 것보다는 복잡합니다.

 

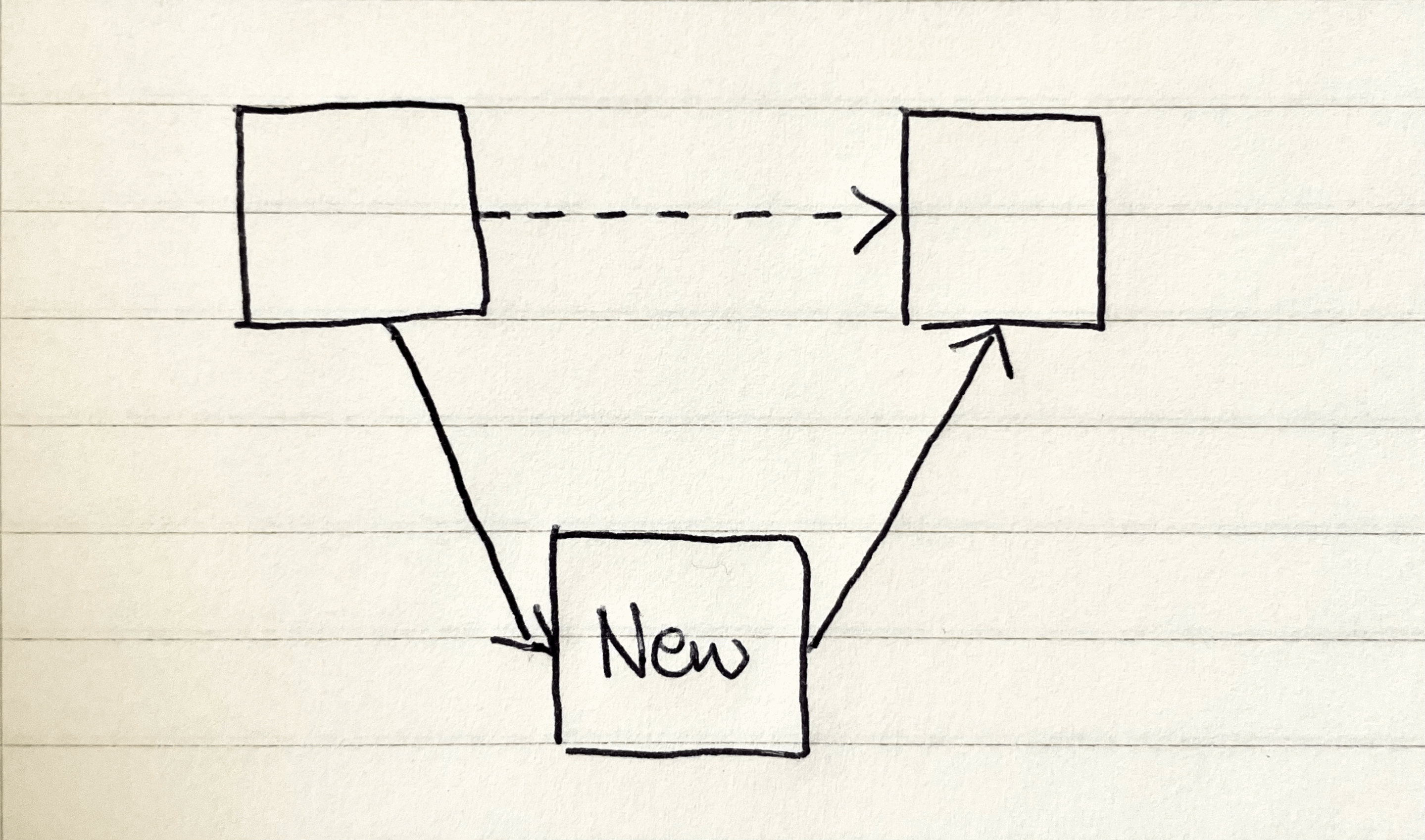
점선이 추가하기 전 연결이고 실선이 추가한 후의 연결입니다.

 

왼쪽 노드의 next를 새로운 노드로, 새로운 노드의 next를 오른쪽 노드로 설정합니다.

위 그림처럼 각 노드가 가리키는 다음 노드만 변경하면 되기 때문에 연산의 오버헤드가 발생하지 않는 것이죠.

맨 뒤 위치에 추가

맨 뒤 위치에 추가하는 것은 tail을 변경하는 것입니다.

현재 tail의 next를 새로운 노드로 설정합니다. 그후 새로운 노드를 tail로 설정합니다.

 

tail을 알기 때문에 단방향 링크드 리스트에서도 O(1)로 맨 뒤 위치에 노드 추가가 가능합니다.

만약 tail을 모른다면 head에서 마지막까지 순차적으로 탐색해야 하므로 O(n)이 소요 됩니다.

 

노드 삭제

노드 삭제는 노드 추가와 반대로 생각하면 됩니다.

head를 삭제한다면 head의 next를 head로 설정합니다.

 

tail을 삭제한다면 tail의 이전 노드를 tail로 설정합니다.

이때, 단방향 링크드 리스트는 n-1번째를 찾아 가야 하지만

양방향 링크드 리스트는 tail의 prev 노드를 이용해 O(1)로 tail 삭제를 할 수 있습니다.

 

중간 노드 삭제는 아래 두 가지 단계를 거치면 됩니다.

• 삭제될 노드의 이전 노드의 next를 삭제될 노드의 다음 노드로 설정한다.
• 삭제될 노드의 다음 노드의 prev를 삭제될 노드의 이전 노드로 설정한다.

 

노드 탐색

링크드 리스트의 탐색은 복잡하지 않습니다.

노드의 next를 이용해 노드 이동을 n번하면 됩니다. 반복문을 이용해 아주 간단히 구현할 수 있습니다.

 

단순한 구현과는 별개로 링크드 리스트에서 노드 탐색은 아주 중요한 연산입니다.

 

링크드 리스트는 중간 노드의 삽입/삭제가 O(1)이라는 장점이 있습니다.

하지만 현실적으로 노드 탐색이 선행되어야 하기 때문에 아주 기초적인 링크드 리스트로는 O(n+1)이 소요됩니다.

따라서 cursor 개념 등으로 최적화를 시켜야 합니다.

 

만약 최적화 과정을 거치지 않는다면 알고리즘에 따라

탐색도 느리고 공간 복잡도도 안 좋은, 배열의 단점과 링크드 리스트의 단점을 모은 최악의 자료구조가 되어 버릴 수 있습니다.

 

최적화 방법은 아래에서 천천히 알아보겠습니다.

 

---

링크드 리스트의 활용

링크드 리스트는 어디에 사용될까요?

 

사실 링크드 리스트는 자주 사용되는 자료구조는 아니라고 합니다. (링크드 리스트를 이용한 스택, 큐, 그래프를 말하는 것이 아닙니다.)

대부분의 상황은 배열과 큰 차이가 없기에 구현하기도 비교적 복잡하고 사용하기도 까다로운 링크드 리스트보다 일반 배열을 사용하는 게 더 편합니다.

또한 다음 노드를 가리키는 주소가 하나라도 잘못 된다면 이후의 모든 연결이 끊어지는 큰 패널티가 있기 때문입니다.

따라서 배열과 비교하면 링크드 리스트가 사용할 때 고려할 점이 많은 것이 사실입니다.

 

운영체제

그럼에도 링크드 리스트는 OS에서 아주 중요한 자료구조로서 동작합니다.

바로 free block을 관리하는데 사용된다는 것인데요. free block은 연속적으로 존재할 수가 없기 때문에 반드시 링크드 리스트를 사용해야 합니다. 이것만으로 링크드 리스트의 존재 가치는 증명이 되었네요!

 

자료구조 최적화

또한 Queue 자료구조도 링크드 리스트를 이용하면 removeFirst( )의 연산 오버헤드를 극복할 수 있습니다.

Queue 포스팅에서 index를 이동하는 것으로 removeFirst( )를 극복하는 사례를 소개하고 직접 테스트도 진행했는데요.

이 방법은 이전 원소들이 모두 남아있기 때문에 공간 복잡도가 좋지 않습니다.

따라서 연결 리스트의 next를 저장하는 것과 이전 원소들이 남아 있는 것의 공간 복잡도를 비교하여

더 유리한 자료구조를 선택한다면 시간 복잡도와 공간 복잡도를 모두 챙긴 Queue를 구현할 수 있습니다.

 

알고리즘

중간 삽입, 삭제가 빈번한 경우에도 유용합니다.

코딩테스트 연습 - 표 편집

2021 카카오 인턴십 문제 중 하나로 이 문제를 배열로 해결한다면 시간 초과가 발생합니다.

중간 삽입, 삭제가 빈번하게 이루어지는데 그럴 때마다 O(n)의 시간이 소요되기 때문입니다.

이럴 때 링크드 리스트를 이용해 문제를 해결하면 됩니다.

 

링크드 리스트의 중간 삽입, 삭제에 대한 시간 측정은 포스팅 가장 아래쪽에 있습니다.

끝까지 읽어주시면 감사하겠습니다 ㅎㅎ

 

 

---

Swift로 양방향 링크드 리스트 구현하기

저는 Swift를 이용해 양방향 링크드 리스트를 구현해보겠습니다.

노드의 추가와 삭제를 구현해 보았습니다.

탐색 연산은 추가와 삭제를 구현하면서 자연스럽게 구현하게 되니 따로 메서드를 정의하지는 않았습니다.

 

제가 스스로 작성한거라 부족한 점이 있을 수 있습니다. 피드백 부탁드려요!

코드 이후에 여러 시나리오에 대해 실행 시간을 비교해보았습니다. 끝까지 봐주시면 감사하겠습니다.

 

Node 클래스

링크드 리스트의 Node 클래스입니다.

class Node {
    var data: Int = -1 //노드의 데이터
    var prev: Node? //이전 노드
    var next: Node? //다음 노드
    
    init(data: Int, prev: Node? = nil, next: Node? = nil) {
        self.data = data
        self.prev = prev
        self.next = next
    }
}

 

양방향 링크드 리스트이기 때문에 next, prev가 존재합니다.

 

LinkedList 클래스

class LinkedList {
    private var head: Node? //맨 앞 노드 => head
    private var tail: Node? //맨 뒤 노드 => tail
    var size: Int = 0 //링크드 리스트의 크기
    var isEmpty: Bool { size == 0 } //링크드 리스트가 비었는가?
    
    ...
}

링크드 리스트의 property 입니다.

맨 앞 노드를 나타내는 head, 맨 뒤 노드를 나타내는 tail이 Node? 형으로 존재합니다.

코드의 가독성과 개발 편의를 의해 size와 isEmpty도 선언해 주었습니다.

 

노드 추가 연산

노드 추가 연산은 맨 뒤에 추가하는 append( )와 특정 위치에 삽입하는 insert( )로 나눠서 구현했습니다.

append( )

//맨 뒤에 노드 추가
func append(data: Int) {
    let newNode = Node(data: data)

    if isEmpty {
        head = newNode
        tail = head
    } else {
        tail?.next = newNode //newNode와 tail을 연결
        newNode.prev = tail
        tail = newNode //tail을 새롭게 설정
    }

    size += 1
}

append( )입니다. 새로운 노드를 맨 뒤에 추가해 줍니다.

링크드 리스트가 비어있다면 head와 tail을 새로운 노드로 설정합니다.

이미 원소가 들어 있다면 next와 prev를 적절히 설정하고 새로 추가한 노드를 tail로 설정해줍니다.

 

append가 끝날 때 size를 1 증가시킵니다.

 

insert( )

//index 위치에 노드 추가
func insert(data: Int, at index: Int) {
    let newNode = Node(data: data)

    if isEmpty { //head가 비어있으면 head로 설정
        head = newNode
        tail = head

        size += 1
        return
    } else if index <= 0 { //head에 추가
        newNode.next = head
        head?.prev = newNode
        head = newNode

        size += 1
        return
    } else if index >= size { //tail에 추가
        append(data: data)
        return
    } else { //중간 삽입
        let half = size / 2
        let isForward = (index <= half)

        var node: Node?
        if isForward {
            node = head
            for _ in 0..<index-1 {
                guard let next = node?.next else { break }
                node = next
            }
        } else {
            node = tail
            for _ in 0..<(size-index) {
                guard let prev = node?.prev else { break }
                node = prev
            }
        }

        node?.next?.prev = newNode
        newNode.next = node?.next

        newNode.prev = node
        node?.next = newNode

        size += 1
        return
    }
}

insert( )입니다. 코드가 참 길죠? ㅎㅎ;;

인자로 받는 index가 head와 가까우면 head부터 next를 이용해 탐색합니다.

tail과 가까우면 tail부터 prev를 이용해 탐색합니다.

 

원하는 위치까지 이동했다면 노드를 연결해주고 size를 1 증가 시킵니다.

중갑 삽입의 최악의 시나리오는 중앙에 삽입을 해주는 것이겠죠?

 

노드 삭제 연산

노드 삭제 연산은 여러 시나리오로 나눴습니다.

모든 노드 삭제, 맨 앞 노드 삭제, 맨 뒤 노드 삭제, 중간 노드 삭제입니다.

 

모든 노드 삭제

//모든 노드 삭제
func removeAll() {
    head = nil
    tail = nil

    size = 0
}

모든 노드를 삭제하는 경우입니다.

head와 tail을 nil로 만들어서 모든 노드가 자연스럽게 ARC에 의해 수거되도록 합니다.

따라서 매우 간편하면서 O(1)로 모든 노드를 삭제할 수 있습니다. ㄴㅇ_ㅇㄱ

 

맨 앞, 뒤 노드 삭제

//맨 앞 노드 삭제
func removeFirst() {
    guard let _ = head else { return }

    head = head?.next
    head?.prev = nil

    size -= 1
    if isEmpty {
        head = nil
        tail = nil
    }
}

//맨 뒤 노드 삭제
func removeLast() {
    guard let _ = tail else { return }

    tail = tail?.prev
    tail?.next = nil

    size -= 1
    if isEmpty {
        head = nil
        tail = nil
    }
}

맨 앞 노드와 맨 뒤 노드를 삭제합니다.

시작할 때 체크하는 head와 tail은 사실 둘 중 어느 것으로 하든 상관 없습니다.

하지만 개념적으로 removeFirst( )는 head를 삭제하는 것이므로 head를 체크하고 removeLast( )는 tail을 삭제하는 것이므로 tail을 체크하였습니다. head, tail이 존재하지 않을 경우 링크드 리스트가 비어있는 것이므로 isEmpty를 이용해서 체크해도 좋습니다.

 

각 노드가 존재한다면 head, tail을 재설정 해주고 size를 조정합니다.

삭제 후 size가 0이라면 안전하게 head와 tail을 nil로 설정해 줍니다.

 

중간 삭제

//index 위치의 노드 삭제
func remove(at index: Int) {
    if isEmpty {
        return
    } else if index <= 0 { //head 삭제
        removeFirst()
    } else if index >= size { //tail 삭제
        removeLast()
    } else {
        let half = size / 2
        let isForward = (index <= half)

        var node: Node?
        if isForward {
            node = head
            for _ in 0..<index {
                guard let next = node?.next else { break }
                node = next
            }
        } else {
            node = tail
            for _ in 0..<(size-index-1) {
                guard let prev = node?.prev else { break }
                node = prev
            }
        }

        node?.prev?.next = node?.next
        node?.next?.prev = node?.prev

        size -= 1
    }

    if isEmpty {
        head = nil
        tail = nil
    }

    return
}

중간 삭제 메서드입니다.

이번에도 head와 가까우면 head부터, tail과 가까우면 tail부터 탐색합니다.

탐색 후 노드를 끊어주고 size를 1 감소 시킵니다.

만약 size가 0이라면 안전하게 head와 tail을 nil로 설정합니다.

 

---

수행 시간 측정

제가 구현한 클래스를 기준으로 수행 시간을 측정해보았습니다.

각 연산은 모두 for문을 이용해 100만회 반복하였습니다.

각 연산이 끝난 후 연산이 정상적으로 완료 되었음을 확인하기 위해 size를 출력하였습니다.

append( ) / removeFirst( )

배열에서 O(1)의 시작이 걸리는 append( )와 O(n)이 걸리는 removeLast( )를 먼저 보겠습니다.

 

append( )는 배열과 마찬가지로 O(1)의 시간복잡도를 가지는만큼 무척 빠른 시간 안에 완료가 됨을 확인할 수 있었습니다.

removeFirst( )은 배열과 반대로 O(1)로 수행이 되기 때문에 append( )와 비슷한 시간으로 완료가 되었습니다.

이로서 맨 앞 원소 삭제는 링크드 리스트가 압도적으로 빠름을 증명하였습니다.

 

insert / remove: 최선의 시나리오

1번 index에 insert와 remove를 해보았습니다.

중간 위치에 삽입, 삭제가 되는 최선의 시나리오입니다.

 

O(1)인 append( ), removeFirst( )와 비슷한 시간으로 수행이 완료되었습니다.

만약 배열이었다면 1회 반복일 때마다 O(n)이 되어 무척 긴 시간이 걸렸을 것입니다.

 

insert / remove: 어중간한 시나리오

그렇다면 어중간한 시나리오는 어떨까요?

앞에서 5번, 뒤에서 5번 Index를 삽입, 삭제 해보았습니다.

 

모두 2초의 시간이 걸렸습니다.

확실히 최선의 시나리오보다 느려진 것을 확인할 수 있었습니다.

 

양방향 링크드 리스트이기 때문에 앞 뒤 연산의 수행 시간이 차이가 없습니다.

만약 단방향 링크드 리스트였다면 앞에서 5번 Index가 훨씬 빠르게 완료되었을 것입니다.

나름의 포인트이니 꼭 확인해 주세요!

 

insert / remove: 최악의 시나리오

이 클래스의 최악의 시나리오는 무엇일까요?

바로 링크드 리스트 중앙 index에 삽입, 삭제가 일어날 경우입니다.

이 시나리오는 100만회를 실행했더니 아무리 기다려도 완료될 기미가 안 보였습니다.

그래서 10만회로 실행해봤지만 그것조차.... ㅠㅠ 그래서 어쩔 수 없이 1만회로 테스트를 했습니다...

 

최악의 시나리오는 아주 기가막힌 실행 속도인 것을 확인할 수 있습니다.

최선의 시나리오와 비교했을 때 100만 분의 1의 연산 횟수지만 실행 속도는 약 10배입니다.

이정도로 느릴 줄은 몰랐는데 저도 참 당황스러웠습니다. 이럴 때 바로 cursor나 center를 이용해 최적화를 해주어야 합니다 ㅎㅎ..

 

---

마무리

오늘은 링크드 리스트에 대해 알아보았습니다.

이전에 알아봤던 배열, 스택, 큐보다는 활용성은 떨어지지만 근본 중의 근본이면서 없어서는 안 될 자료구조입니다.

수행 속도 비교 결과도 참 흥미로웠습니다.

 

잘 쓰면 아주 유리한, 잘못 쓰면 고생만 하는 그런 자료구조가 아닐까 싶습니다.

 

---

잘못된 점이 있다면 댓글로 알려주시면 감사하겠습니다.

감사합니다.